Organic Open-cell Porous Structure Modeling
ACM Symposium on Computational Fabrication 2020
aShandong University bTencent US cDalian University of Technology dThe University of Manchester eThe University of Hong Kong

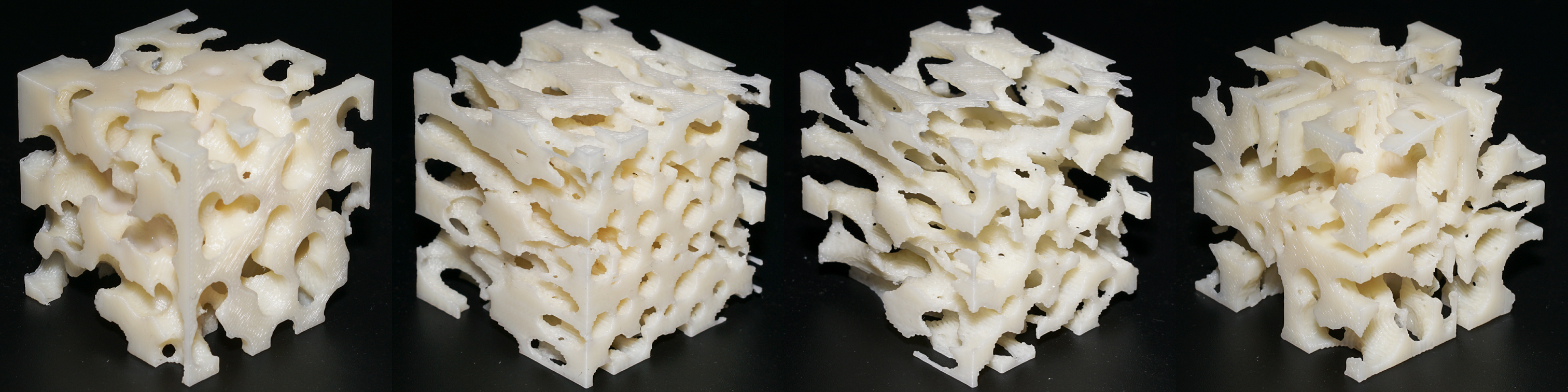
Through the system of this article, from a distribution of particles, we optimize under the
condition of ensuring
its connectivity,
and obtain the corresponding pore structure and solid part of the model.
Abstract
Open-cell porous structures are ubiquitous in nature and have been
widely employed in practical applications. Additive manufacturing
has enabled the fabrication of shapes with intricate interior
structures; however, a computational method for representing and
modeling general porous structures in organic shapes is missing in
the literature. In this paper, we present a novel method for modeling
organic and open-cell porous structures with porosities and pore
anisotropies specified by users or stipulated by applications. We
represent each pore as a transformed Gaussian kernel whose
anisotropy is defined by a tensor field. The porous structure is
modeled as a level surface of combined Gaussian kernels. We utilize
an anisotropic particle system to distribute the Gaussian kernels
concerning the input tensor field. The porous structure is then
generated from the particle system by following the anisotropy
specified by the input. We employ Morse-Smale complexes to
identify the topological structure of the kernels and enforce pore connectivity. The resulting
porous structure can be easily controlled
using a set of parameters. We demonstrate our method on a set
of 3D models whose tensor field is either predesigned or obtained
from the mechanical analysis.
More Results




Downloads
Acknowledgement
We thank all the anonymous reviewers for their valuable comments and constructive suggestions. This work is supported by grants from NSFC (61972232) and State Key Laboratory of Virtual Reality Technology and Systems (VRLAB2019A01).
BibTex
@inproceedings{Tian2020Porous,
author = {Tian, Lihao and Lu, Lin and Chen, Weikai and Xia, Yang and Wang, Charlie C. L. and Wang, Wenping},
title = {Organic Open-Cell Porous Structure Modeling},
year = {2020},
isbn = {9781450381703},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3424630.3425414},
doi = {10.1145/3424630.3425414},
booktitle = {Symposium on Computational Fabrication},
articleno = {9},
numpages = {12},
location = {Virtual Event, USA},
series = {SCF '20}
}


