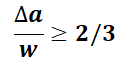问题描述:
给定确定体积的陶泥(打印长度确定),学员自行设计打印路径,使得打印出的陶泥模型满足约束条件;设计的路径保存为G-code文件。
约束条件:
1.全部打印路径为空间中一条连续的路径
2.模型需要自支撑
3.打印路径不能发生自交
陶泥打印机介绍:
-打印机尺寸:
CERAMBOT Plus打印机最大打印尺寸为:180*190*200mm,大家需要按照该尺寸设置打印中心。此外,为了保证打印时间,我们推荐大家设计模型时将尺寸控制在120*120*120mm以内。
-线宽
因为陶瓷打印的陶瓷浆料的挤出量通常大于其他增材制造方式,所以打印路径中每个移动步骤的挤出量计算是一个关键问题。挤出量不足会导致相邻层的支撑较少,从而导致模型坍塌,如图1所示。另一方面,过多的挤出量导致粗糙的表面质量和更多的打印制造时间,从而导致陶瓷制品的不确定性。因此,需保证挤出量自适应,防止模型坍塌。
 |
|
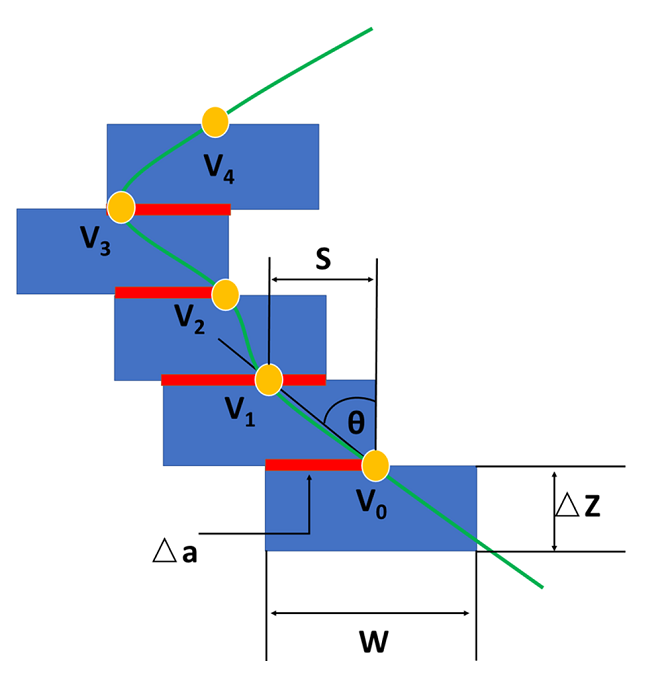 |
图1 自适应挤出量对比效果 |
|
图2 自适应挤出计算原理 |
如图2所示,两个相邻点的水平距离用s表示,两个相邻层的重叠宽度用∆a表示,w是直写线条宽度。θ是点的切线与打印方向之间的角度,θ最好不要超过30°,极限45°,否则,模型需要支撑才能避免坍塌。因此,根据角度限制,我们可以将比例阈值设置为2/3,即满足如下公式:
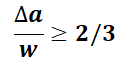
-G-code规范:
G-code是控制陶瓷打印成型过程的一系列命令,控制陶瓷打印设备的运动,例如移动的位置,使用的速度等等,每一行的打印指令在打印G代码中占据一行。
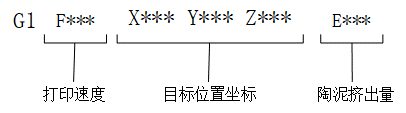
如上图所示的示例命令,参数X、Y、Z分别表示打印喷头的目标位置的坐标值,当运行到该指令时,打印喷头将从当前的位置移动到目标位置。参数E代表陶瓷浆料的挤出量,为从开始到当前层的陶泥累积挤出量。 某一行G-code的E值相较于上一行E值的增量表示为该步的陶泥挤出量e。
特别地,仅在G1时才会出现E值,若执行命令开始为G0,则将不进行陶瓷挤出,只进行打印喷头的移动。参数F表示打印的直线段XYZ的运动速度,单位是mm/min,在此处我们推荐为F=1800。同时,如果某条执行指令中不包含F参数时,则该直线段内的打印速度和上一步打印速度相同。
在生成G-code的工作中,要计算每个步骤的路径以及挤出量。如图3所示。这里,V0和V1表示路径上的两个相邻打印点,两点间距离L即为喷头移动步长。V0和V1的平均直写线条宽度用w表示,平均层高为∆z。V0到V1的最终挤出量e近似于黄色长方体的体积,即:
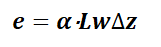
其中为打印机内参系数,此处为一常数。

图3 挤出量示意见图
为了计算挤出量e,需要确定层高∆z0,直写线条宽度w的数值。这些参数主要由挤出机喷头的内径确定。在本研究的设置中,我们建议设置参数如下:∆z0 =1.2mm,w = 3mm,F=1800,α=0.4。
在相同速度F和层厚下,挤出量越大,线宽w越大。
-注意事项:
需要在生成的G-code前添加:
G28 ;Home
G1 Z15.0 F1800 ;Move the platform down 15mm
;Prime the extruder
M302
G1 F1800 E3
G92 E0
需要在生成的G-code末尾添加:
M104 S0
M140 S0
;Retract the filament
G92 E1
G1 E-1 F300
G28 X0 Y0
M84
教程最后为示例模型和其对应的标准G-code。“;”后为注释代码。
可以安装repetier或者Cura进行G-code预览:
repetier: https://www.repetier.com/download-now/
Cura: https://ultimaker.com/software/ultimaker-cura
路径设计思路:
学员们可以从以下多个角度来设计G-code路径:
01.Simple cylinder(简单柱体):
对于一些简单柱体,学员们可以直接生成对应的G-code:
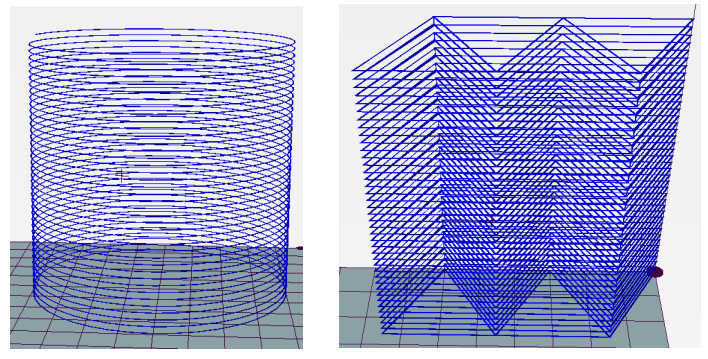
生成圆柱坐标点的示例代码:main.cpp
#include
#include
#include "tool.h"
using namespace std;
class Point3f
{
public:
Point3f(){};
Point3f(float num1, float num2, float num3)
{
x = num1;
y = num2;
z = num3;
}
Point3f operator + (const Point3f &a)
{
return Point3f((a.x + this->x), (a.y + this->y), (a.z + this->z));
}
float x, y, z;
};
int main()
{
vector<vector<Point3f>> a;
Point3f shift(100, 100, 0); //将模型中心移动到打印托盘中心
//cylinder
double radius = 40;//半径40mm
int layer_num = 30;
int interval = 40;
double angle_add = 360 / interval;
double zz = delt_z / interval;
for (int i = 0; i < layer_num ; i++)
{
vector<Point3f> b;
for (int j = 0; j < interval; j++)
{
double angle = angle_add * j;
b.push_back(Point3f(radius*cos(angle*PI / 180), radius*sin(angle*PI / 180), i * delt_z + j * zz) + shift);
}
a.push_back(b);
}
string file = "D://example1.gcode";
vector_to_gcode(a, file);
return 0;
}
根据坐标点生成G-code的代码:tool.h
#ifndef TOOL_H
#define TOOL_H
#include <iostream>
#include <fstream>
#include <string>
#include <vector>
using namespace std;
static double Wmin = 3; //measurement: mm
static double delt_z = 1.2;
static double lamda = 0.4;
#ifndef PI
#define PI 3.1415926535897932384626433832795
#endif
template
void vector_to_gcode(vector> contours, string filepath)
{
double E = 0;
ofstream out(filepath);
if (out.is_open())
{
out << "G28 ;Home \nG1 Z15.0 F1800 ; Move the platform down 15mm \n;Prime the extruder \nM302 \nG1 F1800 E3 \nG92 E0 " << endl;//contours[0].size()
}
out << "G0 X" << contours[0][0].x << " Y" << contours[0][0].y << " Z" << contours[0][0].z << endl;
int sizev = contours.size();
T last_one;
for (int i = 0; i < sizev; i++)
{
int size_one = contours[i].size();
if (i == 0)
{
for (int j = 1; j < size_one; j++)
{
double length = length_P(contours[i][j - 1], contours[i][j]);
double e = lamda * length * Wmin * delt_z;
E += e;
out << "G1 X" << contours[i][j].x << " Y" << contours[i][j].y << " Z" << contours[i][j].z<< " E" << E << endl;
}
last_one = contours[0][size_one - 1];
}
else
{
for (int j = 0; j < size_one; j++)
{
double length = length_P(last_one, contours[i][j]);
double e = lamda * length * Wmin * delt_z;
E += e;
out << "G1 X" << contours[i][j].x << " Y" << contours[i][j].y << " Z" << contours[i][j].z << " E" << E << endl;
last_one = contours[i][j];
}
}
}
out << "M104 S0 \nM140 S0 \n;Retract the filament \nG92 E1 \nG1 E-1 F300 \nG28 X0 Y0 \nM84" << endl;
cout << "Write done!" << endl;
}
template
double length_P(T a, T b)
{
return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y) + (a.z - b.z)*(a.z - b.z));
}
#endif
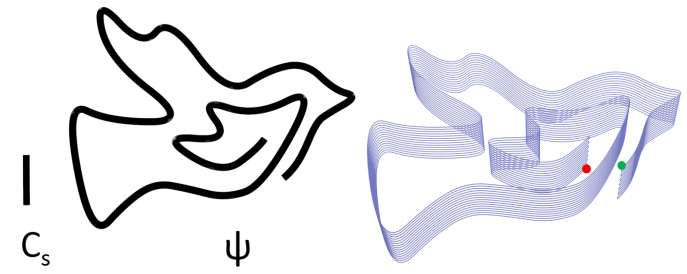
02.Sweeping surface(扫掠面):
学员们可以选择任意一条曲线Cs, 将Cs沿着路径曲线ψ进行扫掠,计算每一层点的位置,然后根据坐标点生成G-code文件(同01: tool.h)。
学员在扫掠过程中可以对Cs进行调整,包括长度和形状。也可以通过控制挤出量来控制层厚,进而获得不同的打印效果。
03.Modeling and Slicing(建模—切片):
学员们可以使用建模软件设计模型,通过切片得到对应的G-code。由该方法生成路径时,需要保证路径满足前文提到的三条要求。
本课题不限制生成G-code的方法,学员们可以使用上述方法或者其他任何方法生成你们想要的G-code。
问题描述:
学员首先学习了解TPMS的相关基础知识,在一个基于libigl的基础框架上,进行TPMS结构的设计,利于相关软件(如maya,magics等)生成基于该TPMS结构的多孔模型,并利用提供的3D打印机进行制造。
下载配置libigl
下载libigl:https://github.com/libigl/libigl
或使用git: git clone https://github.com/libigl/libigl.git
使用cmake进行编译
在编译时会下载libigl所需的外部依赖项,github传输不稳定时,可将./cmake/LibiglDownloadExternal.cmake内GIT_REPOSITORY替换为国内源。
可用教程内LibiglDownloadExternal.cmake进行替换
学员也可参考以下博客进行libigl的安装配置:
https://blog.csdn.net/u014354193/article/details/73380249
生成TPMS网格模型
-TPMS
TPMS(Triply periodic minimal surface),是极小曲面中的一种,可参考论文
[Computer-aided porous scaffold design for tissue engineering using triply periodic minimal surfaces](https://link.springer.com/article/10.1007/s12541-011-0008-9),了解TPMS生成原理。
以下是一些关于如何生成TPMS的介绍:
https://wewanttolearn.wordpress.com/2019/02/03/triply-periodic-minimal-surfaces/
-Marching cube算法
Marching cube是经典的重建算法,可以用来生成隐式方程所表达的surface,算法流程可参考论文:[Marching cubes: A high resolution 3D surface construction algorithm]
(https://dl.acm.org/doi/10.1145/37401.37422)
本次实验中可以使用libigl中提供的marching_cubes 函数:https://libigl.github.io/tutorial/#marching-cubes
-具体操作步骤
1.选定一种TPMS表达函数(隐式方程)进行编码;
2.使用libigl提供的marching cube算法,设定设置合适的函数周期和重建坐标范围;
3.计算对应voxel的坐标及TPMS在此位置的函数值,生成scalar field 'S' 和 vertex locations 'GV'
4.利用对应函数生成TPMS网格模型并绘制查看效果,将结果保存为obj格式。

TPMS函数
关键代码:
计算TPMS在某位置的函数值:
double TpmsValue(Vector3d coord, TpmsType tpms_type_)
{
double x = coord[0], y = coord[1], z = coord[2];
double tpms_value = 0;
double tpms_constant_ = 0;
if (tpms_type_ == kP) tpms_value = cos(x) + cos(y) + cos(z) + tpms_constant_;
……
……
return tpms_value;
}
划分voxel:
int count_num = x_voxel_num*y_voxel_num*z_voxel_num;
MatrixXd GV(count_num, 3);
for (int zi = 0; zi < z_voxel_num; zi++)
{
const double z = (double)zi/(z_voxel_num-1) * model_size;
for (int yi = 0; yi < y_voxel_num; yi++)
{
const double y = (double)yi / (y_voxel_num - 1) * model_size;
for (int xi = 0; xi < x_voxel_num; xi++)
{
const double x = (double)xi / (x_voxel_num - 1) * model_size;
GV.row(xi + x_voxel_num*(yi + y_voxel_num*zi)) = Vector3d(x, y, z);
}
}
}
计算scalar field 'S':
VectorXd S(count_num, 1);
for (int n = 0; n < count_num; n++)
S(n) = TpmsValue(GV.row(n), kTubularG);
用Marching Cube算法计算结果:
MatrixXd SV;
MatrixXi SF;
igl::copyleft::marching_cubes(S, GV, x_voxel_num, y_voxel_num, z_voxel_num, SV, SF);

由Tubular G重建生成的网格模型
模型求交
将TPMS模型与其他模型求交,可使用magics,maya等软件。得到TPMS多孔模型。
i. 导入模型(maya只接受obj格式文件)

ii. 移动模型至相交位置(maya快捷键w-平移,e-旋转,r-缩放,alt+鼠标控制视图),同时选中两个模型,选择“网格—布尔—交集”,点击后面方框进行设置,选择“正常”。
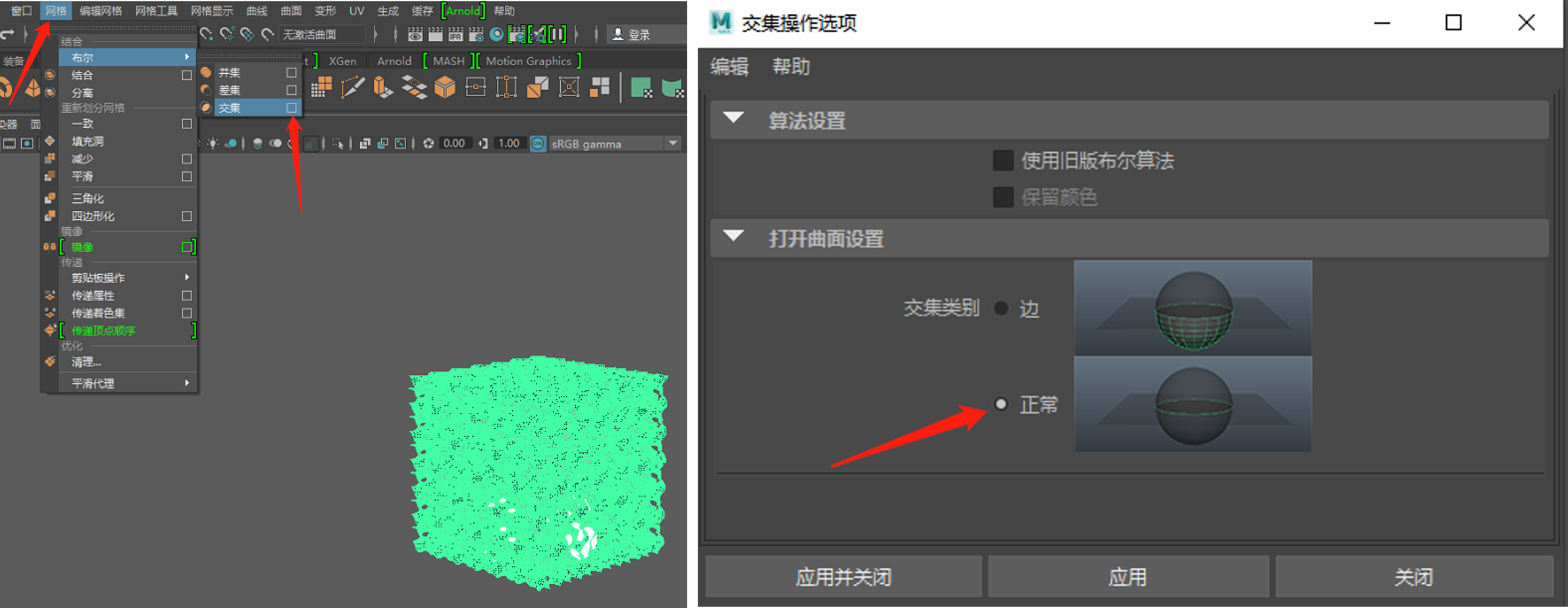
iii. 得到多孔模型

bunny多孔模型
iv. 利用Autodesk Meshmixer为模型挤出厚度,首先导入模型
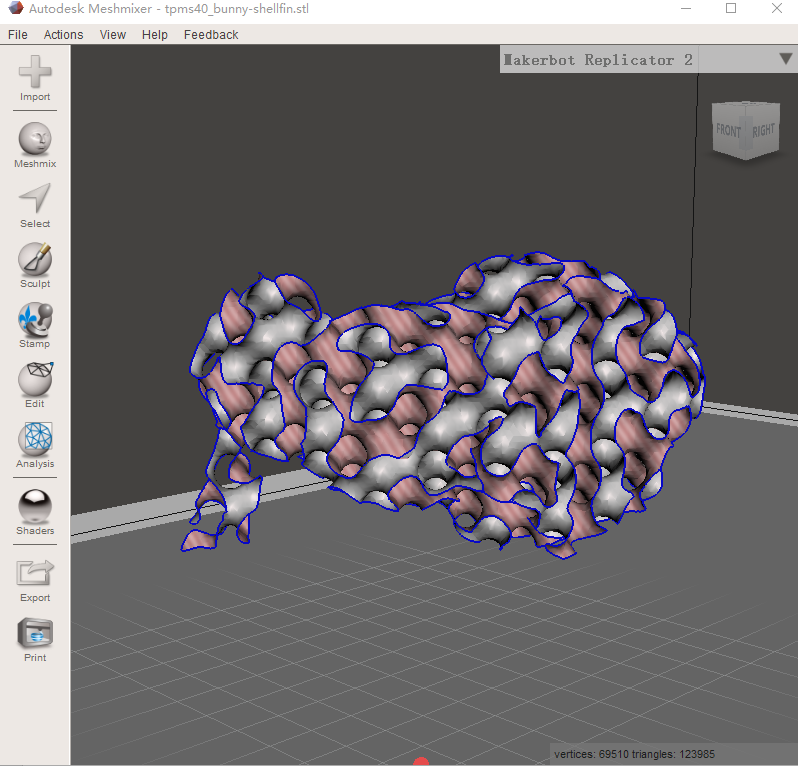
导入模型
v. Ctrl+A,全选模型,选择“Edit—>Extrude”功能,设置“Direction”和“Offset”等参数

vi. 将模型用F170打印机打印出来。