1. 组装外壳并建模,操作打印机:
首先我们会提供部分扫描仪部件,然后需要学员将现有的外壳零件组装在一起,并使用Maya进行三维建模,得到扫描仪额外需要的各零件的STL模型,并使用给定的3D打印机将零件打印出来,最后测量相应固定参数供其他模块使用。
这里我们提供了两台不同类型的打印机,对应的打印机操作指南如下:
Flashprint-UserGuide.pdf (2.4M)
makerbot-UserGuide.docx(0.3M)
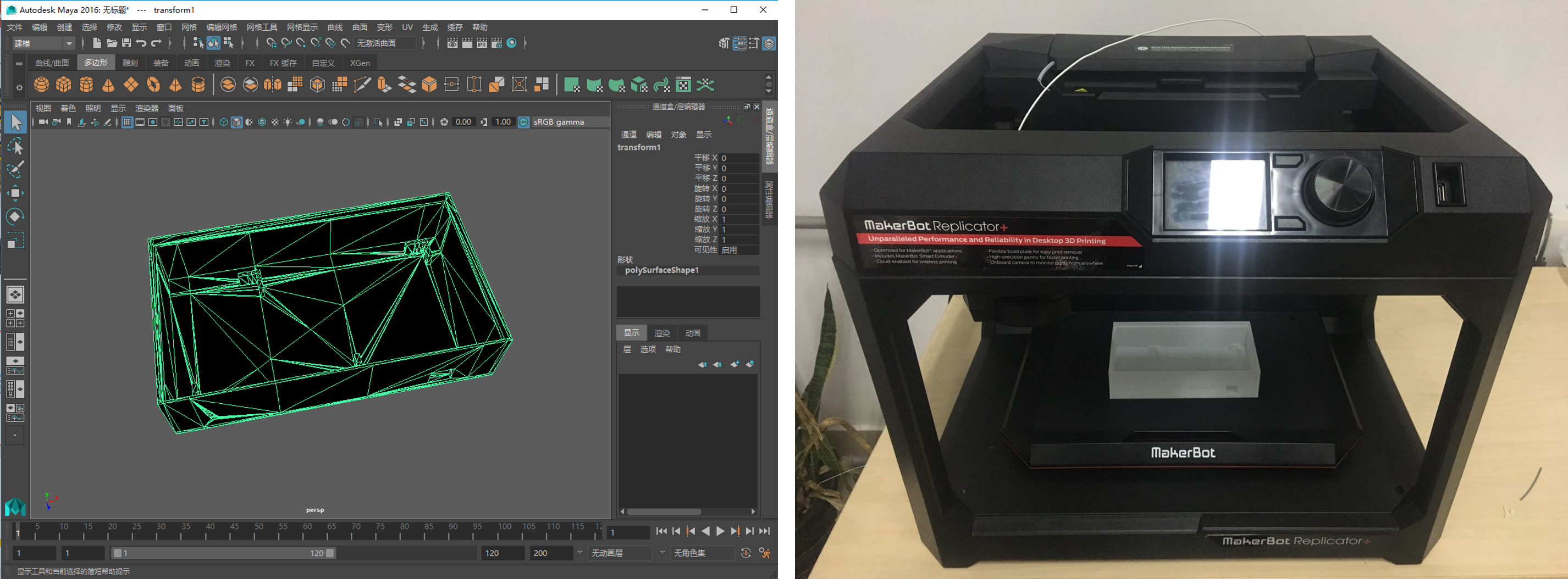
扫描仪部件的建模及打印
将扫描仪欠缺部件打印出来后,学员按照说明将扫描仪组装完毕。组装说明参见: FabScan组装 及 FabScan项目主页 。
2. Arduino编程,调试,实现运动及开关控制:
-Arduino软件及其驱动安装步骤:
扫描仪组装完毕后,学员通过Arduino编程,调试,实现舵机及其他部件的运动及开关控制。首先需要安装Arduino软件,然后为Arduino板子安装驱动,详情见教程: Arduino软件及其驱动安装步骤 (0.4M) 。

本次DIY所使用的Arduino UNO板子
-Arduino编程,调试:
驱动安装成功后,学员首先通过一个 "Hello World" 程序了解Arduino编程,然后根据之后的 Arduino控制教程 (0.6M)进行编程,来控制舵机,激光器,以及串口通信,其中串口通信部分可以参考 SerialPort.zip (0.1M)中的程序。
3. 下载配置libigl
-libigl介绍:
libigl 是一个由 Daniele Panozzo and Alec Jacobson 开发的用于图形处理的c++开源库,适合于初涉图形处理的同学们使用。相对于传统的图形图像处理库,比如CGAL,openmesh等,libigl 抛弃了复杂的数据结构,基本数据结构依赖于eigen,一个类似于MATLAB风格的C++数学库。除此之外,libigl还是header-only的,并且有详细且易于理解的tutorial,特别适合初学者对图形处理的基本操作进行理解。当然libigl自带的简单、易于交互的图形界面也是其一大风格。
在这一步,学员需要利用C++图形处理库libigl编写图形界面,作为主程序,并预留程序接口,用于整合图像处理,测距算法,Arduino串口通信等各个模块。
-下载:
下载libigl:https://github.com/libigl/libigl
或使用git: git clone https://github.com/libigl/libigl.git
-编译:
下载完毕后,学员可使用cmake-GUI进行编译。
CMAKE是一种比较高级的编译配置工具,它首先允许开发者编写一种平台无关的CMakeList.txt文件来定制整个编译流程,然后再根据目标用户的平台进一步生成所需的本地化Makefile和工程文件。CMake的下载地址为https://cmake.org/download/ 。
使用CMake打开../libigl/tutorial文件夹,并在文件夹内新建build文件夹。由于libigl使用了一些c++11 的新特性,在Windows上只能使用VS2015 64 位及以上版本进行编译。点击configure,第一次编译肯定是失败的,不要着急。
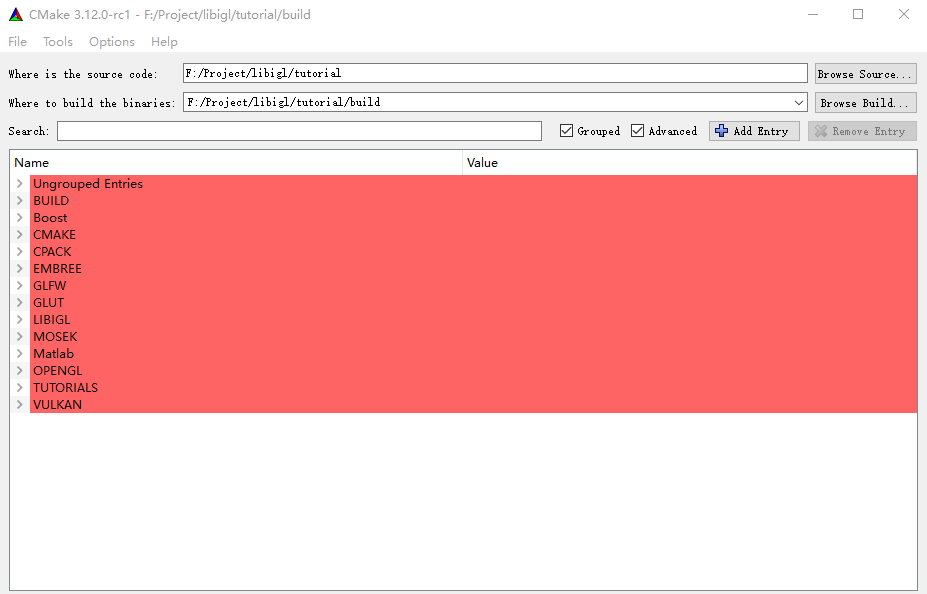
打开名为libigl的下拉菜单,会发现其中有若干选项。第一项 LIBIGL_USE_STATIC_LIBRARY 决定你是否使用静态编译,两者皆可。由于LIBIGL_WITH_CGAL、LIBIGL_WITH_MATLAB 调用的是编译好的lib,所以需要先安装CGAL和MATLAB在进行配置,因此比较麻烦,所以没有需要不用勾选此项。此外,对于基本的GUI界面和基本操作,LIBIGL_WITH_OPENGL_GLFW_IMGUI也是需要勾选的。其余是默认的即可。
再次点击configure进行编译,这次没有标红。然后点击generate。
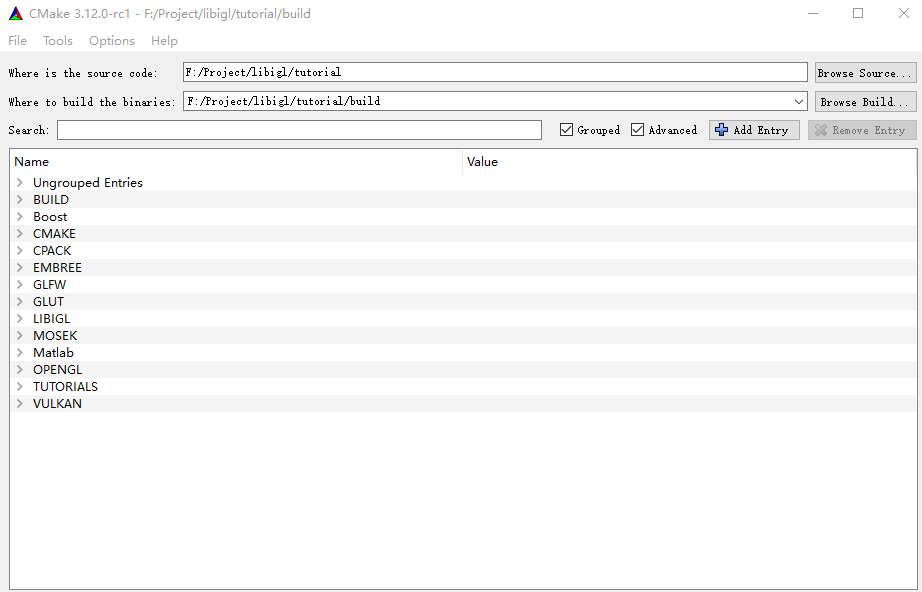
现在使用VS2015打开任意example都可以进行单独编译,这里对106进行单独编译,结果如下:

学员也可参考以下博客进行libigl的安装配置: https://blog.csdn.net/u014354193/article/details/73380249。
更多libigl的使用教程可以参考libigl中tutorial文件夹,其中101_FileIO, 102_DrawMesh, 106ViewerMenu可以涵盖本次DIY所需的功能。
Tips: 使用libigl显示点云方法:
Eigen::MatrixXd V1;
int r = 0;
int g = 0;
int b = 0;
viewer.data.add_points(V1, Eigen::RowVector3d(r, g, b));
可在OpenGL_state.cpp 内的IGL_INLINE void igl::viewer::OpenGL_state::draw_overlay_points(){}方法内使用 glPointSize(3);进行点大小的设置。
4. 相机标定及光点坐标求解
-Camera Calibration:
现实的摄像机都是采用光学透镜聚光成像的,并且所用的透镜由于加工工艺限制不可能是严格的抛物面,同时, 感光芯片也透镜之间也非严格平行。因此我们使用的摄像机所产生的画面实际上是存在扭曲和偏移的,如果直接使用原始的摄像机画面进行测距,势必造成误差。 因此学员需要按照 Camera Calibration Toolbox 教程进行相机的标定,通过标定后获取消除画面中的扭曲和偏移,再进行激光测距的相关操作。

-激光光点像素坐标确定和求解:
希望从摄像头拍摄的画面中得到一字线激光每个光点的坐标信息, 需要解决两个问题:
1. 识别激光线;
2. 确定激光线每个光点的坐标。
对于第一个问题,可以分析图片的像素分布,确定激光线的像素特征,从而可以将图片进行二值化处理,以便下一步提取光点坐标。对于第二个问题,可以逐次分析每行像素,提取激光线的中心点作为激光点的坐标。
该部分的输入是相机拍摄的画面,输出是一组激光点在图像上的坐标。
此外,为了能够进行三角测距,需将激光点在图像上的坐标转换为在相机成像传感器上的坐标。可用如下相似关系进行转换。
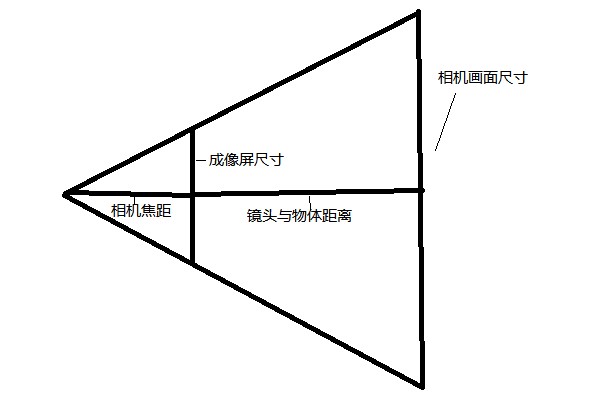
相似关系转换
5. 扫描并进行测距
本部分程序所需输入为照片中激光点的像素坐标,输出为三维空间中的点位置。算法基本原理为三角测距。
-原理和算法:
这里先介绍测量目标上一个点所涉及的算法。3D扫描将采用类似的方式进行扩充。
使用单点激光进行三角测距:
除了使用相位差和时间差进行TOF测距外,另一种测距方式就是三角测距。这也是实现低成本激光测距的关键,因为这种方式不需要具备其他测距方式所要求的特殊硬件。并且,在一定距离范围内, 三角测距也可以达到与TOF测距媲美的测量精度和分辨率。
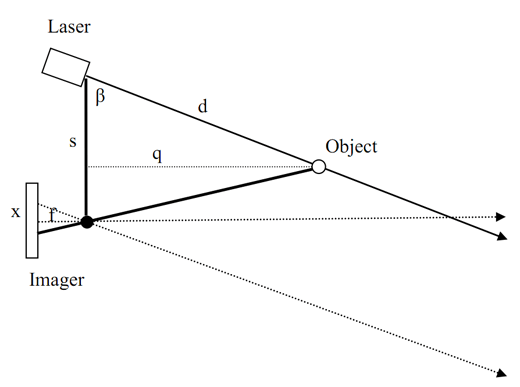
激光三角测距原理
这里摘录了论文中的示意图,要进行激光三角测距,所需的设备很简单: 点状激光器、摄像头。因此,能做到多少的成本大家现在应该比较清楚了。图中展现了测量对象Object距离激光器的距离d的示意图。图中的Imager部分是对摄像头的一种抽象表达(针孔摄像机模型)。标有s的线段实际可以是一个固定摄像头和激光器的平面。摄像头成像平面与该固定平面平行,而激光器发出的射线与该平面夹角beta仅存在于图中的视图中
要测量距离d,首先要求激光射线射到了Object上,他的反射光在摄像头的感光平面上成像。对于不同远近的物体,当被测距激光照射后,摄像头上的成像光点的x值将变化。这里涉及到如下几个参数:
Beta:激光器夹角
s:激光器中心与摄像头中心点距离
f:摄像头的焦距
如果这些参数在测距设备安装后不再改变(固定)且数值已知,则物体距离激光器距离可由如下公式求得:
q=fs/x .... (1)
d=q/sin(beta) .... (2)
其中,x是测量中唯一需要获得的变量。它的含义是待测物体上激光光点在摄像头感光元件(如CMOS)上的成像到一侧边缘的距离。该距离可以通过在摄像头画面中查找并计算激光点中心位置的像素坐标来求得。
式(1)求出了目标物体与摄像头-激光器平面的垂直距离(实际上对于大尺度测距,该值可以近似认为是实际距离)。这一步就是三角测距的所有内容了,非常简单。
不过,在实际操作中,上述公式仍旧需要扩充。首先时对于变量x的求解,假设我们已经通过算法求出了画面中激光光点的像素坐标(px,py),要求出公式中需要的x,首先需要将像素单位的坐标变换到实际的距离值。为了计算方便,在安装时,可以令摄像头画面的一个坐标轴与上图线 段s平行,这样做的好处是我们只需要通过光点像素坐标中的一个参量(px或者py)来求出实际投影距离 x。这里假设我们只用到了px。
那么,变量x可以由如下公式计算;
x=PixelSize*px+offset .... (3)
式(3)由引入了两个参数,PixelSize以及offset。其中PixelSize是摄像头感光部件上单个像素感光单元的尺寸,offset是通过像素点计算的投影距离和实际投影距离x的偏差量。这个偏 差量是由如下2个因素引入的:
1. x变量的原点(示意图中与激光射线平行的虚线和成像平面交点)的位置未必在成像感光阵列的第一列(或排)上(实际上在第一排的概率非常低)
2. 通过摄像头主光轴的光线在画面中的像素坐标未必是画面中点。
对于PixelSize,可以通过摄像头感光元件手册来确定其数值。对于offset,要在安 装上消除offset或者直接测量,在其余条件下几乎是不可能的,因此,需要通过后面介绍的矫正步骤求出。到这里,我们得出了通过激光点像素坐标(pX)来求出对应光点实际距离的公式:
d=fs/(PixelSize*px+offset)/sin(beta) .... (4)
接下来的问题就是如何确定这些参数了。
-3D激光扫描的原理:
由前文已经指出,这里采用了线状激光器一次对一条线而非单点的目标物体进行扫描测距。将扫描器进行旋转,从而可以实现3D扫描。下图展示了他的工作画面和捕获到的摄像头画面 :
 |
 |
本制作早期使用的红色一字线激光器的工作画面 |
采用红色一字线激光器捕捉到的画面 |
对于线状激光器进行测距的问题,可以将它转化为前面单点激光测距的计算问题。对于上图中的激光线条,算法将按照Y轴依次计算出当前Y轴高度下,激光光斑的X坐标值pX。并尝试通过先前的算法求处该点的距离。为了简化问题,我们先考虑对于一个与摄像头感光面平行的平面上激光光斑各点的 距离问题:
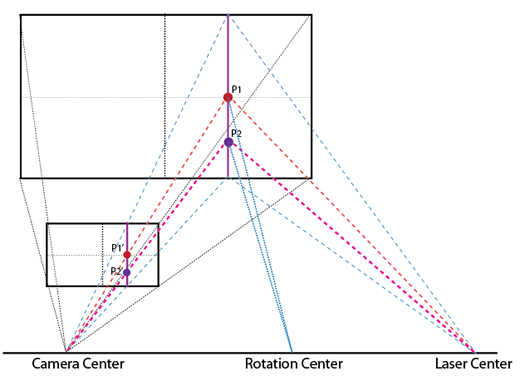
激光线条光斑在平行平面上各点的距离问题抽象
如上图所示,远处平面为目标待测平面,上面有一条紫色的激光光斑。近处的平面 是摄像头的感光成像平面,经过了翻折后,他可以看作是目标平面到摄像头成像中心点组成的棱锥的一个截面。图中的P1点位于摄像头投影画面高度的中点,按照针孔摄像机的定义,该点在画面上的投影P1'距离摄像头中心Camera Center的距离应当为摄像头的焦距F。因此,对于P1,可以直接带入式(4)求出实际距离。
现在的问题是,对于其他高度上的点,如P2,是否可以通过式(4)求得?
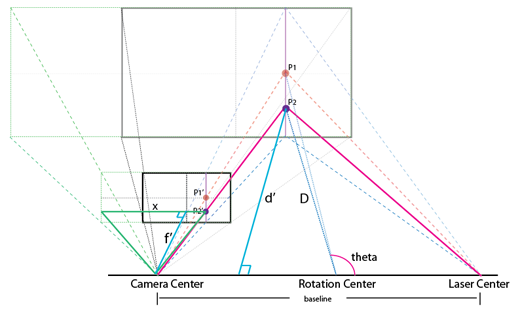
3D测距的原理
答案自然是肯定的,不过这里涉及到了额外的参数。如上图所示,设P2的投影点P2' 到摄像头中心距离为f',则P2到baseline垂线距离d'可由如下公式得到:
d'=f'baseline/x .... (6)
而很容易知道,f'可以通过f求出:
f'=f/cos(arctan((P2'.y-P1'.y)/f)) .... (7)
其中的P2'.y以及P1'.y分别是点P2',P1'在成像元件上的实际高度,他们可由各自点像素坐标P.y乘以像素高度求出。
在求出了垂线距离d'后,需要转化成实际的距离D,此时需要知道P2-RotationCenter以及Baseline组成的夹角theta。该角度可以由立体几何知识通过激光器与 Baseline的夹角beta求出。具体的求解公式可以参考本制作配套源代码的计算部分。
在求出了平行平面上激光光斑任意点的坐标后,可以将问题一般化,对于3D空间任意激光投影点,可以先构造出该点所在的一个平行平面,然后利用上述算法求解。对于每次测距采样,上述算法将产生一个数组dist[n]。其中 dist[i]为对应画面不同高度像素坐标i下激光点的距离。对于采用640x480分辨率的摄像头,n的取值 为480。
如果进行180度,步进为1度的3D扫描,则可得到分辨率为 180x480的点云阵列。如果采用0.3度步进,扫描180度,则得到600x480的点云阵列。
-测距参数校正:
需要校正的参数请参考前篇“相机标定及光点坐标求解”。要开始测距校正,首先要求PC客户端软件已经能够得到激光光斑中心位置了。这里给出对画面中心位置激光光斑测距参数校正的过程。其他的参数可以用相同的思路进行。
理想的校正环境是比较空旷的区域,前方有垂直的白墙用于反射激光光斑。并配备测距仪器:卷尺。
6.点云重建,得到曲面信息
三维激光扫描和建模技术可以快速获取现实世界中真实物体表面的精确几何信息,它可以深入到复杂的现场环境及空间中进行扫描操作,并直接将各种大型的、复杂的、不规则、标准或非标准等实体或实景的三维数据完整地采集到电脑中,从而快速重构出目标的三维模型,并能获得三维空间的线、面、体等各种制图数据,同时,它所采集的三维激光点云数据还可进行多种后处理工作,如测绘、计量、分析、仿真、模拟、展示、监测、虚拟现实等。构建点云拓扑信息的三角网算法,以 Delaunay算法最为经典,鲁棒性最强。在 Delaunay 的各种算法中,AMENTA 等人提出的PowerCrust 算法最为著名。
-powercrust 三维重建原理:
PowerCrust 其利用中心轴变换得到物体表面,物体结构是由位于物体里面与外面极点子集确定的。这些极点集(如 Voronoi 图表)将空间分为许多多面栅格,内部栅格结合的边界就会构成多边形的输出表面或 PowerCrust 。孔穴中,内部极点球状物能凸出物体的外面,外部的极点球状物能凸出里面。PowerCrust 能生成密封模型,模型中输出 3D固体周界面,能创建出一个正确、会聚性强的复杂物体模型。密封模型使用广泛,可为物体限定的元素分析所创建网格构造;为分层的制造加工、快速成型创建 STL 模型。PowerCrust 通过收缩内部球体,并膨胀相同数量的外部球体,能建造许多 CAD 程序粗糙,偏差大的外表面。该算法具有很强的理论支持,对任意散乱点云输入,它都能获取致密的表面,同时避免以前同类算法的多边形化,孔洞填补以及后期处理等操作,具有相当强的鲁棒。该算法对具有锐利边缘的物体,采样密度不均匀的散乱点集以及高噪声散乱点集也都有较好的处理效果。
-算法步骤:
PowerCrust 算法的具体实施步骤如下:
(1)对采样点集 S 进行 Delaunay 三角剖分,计算其对应的 Voronoi 图;
(2)计算每个采样点的极点;
(3)计算极点的 Power 图;
(4)标记出极点是属于内部还是外部的;
(5)输出:分离内外极点的 Power 图的平面,生成近似曲面(PowerCrust);内部极点的三角剖分的面,得到内部中轴的近似值(PowerShape)。