Revisiting Stress Majorization as a Unified Framework for
Interactive Constrained Graph Visualization
IEEE Transactions on Visualization and Computer Graphics (Proc. InfoVis 2017), 2018
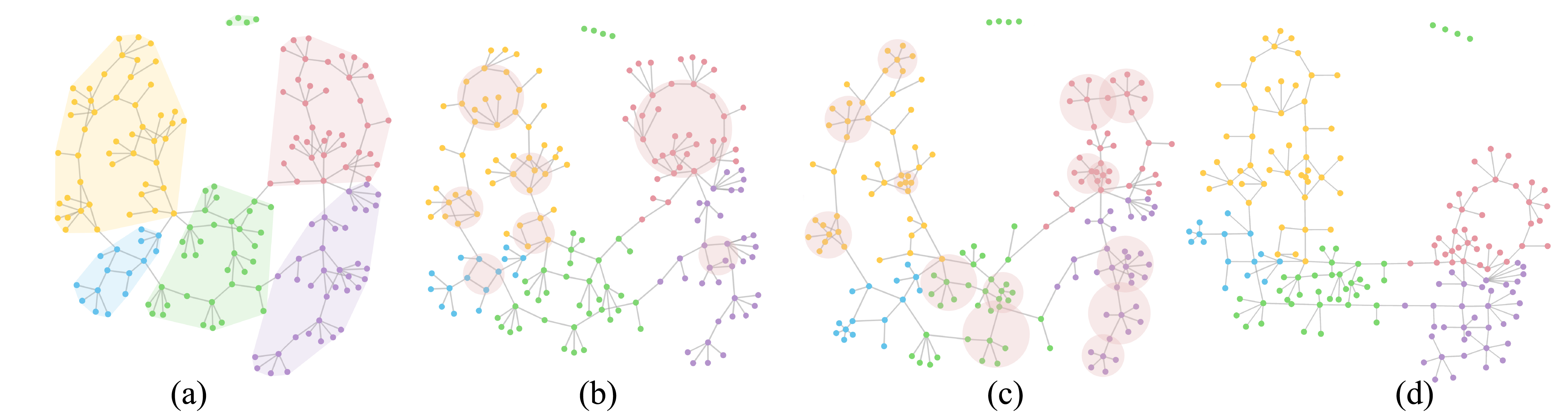
Figure 1: Our unified framework for constrained graph visualization allows us to create graph layouts with various constraints: a) cluster non-overlap (CN); b) CN + circle constraint (CC); c) CN + star constraint (SC); and d) CN + CC + SC + edge direction constraint.
Abstract:
We present an improved stress majorization method that incorporates various constraints, including directional constraints without the necessity of solving a constraint optimization problem. This is achieved by reformulating the stress function to impose constraints on both the edge vectors and lengths instead of just on the edge lengths (node distances). This is a Unified framework for both constrained and unconstrained graph visualizations, where we can model most existing layout constraints, as well as develop new ones such as the star shapes and cluster separation constraints within stress majorization. This improvement also allows us to parallelize computation with an efficient GPU conjugant gradient solver, which yields fast and stable solutions, even for large graphs. As a result, we allow the constraint-based exploration of large graphs with 10K nodes – an approach which previous methods cannot support.Video:
Download MP4[56M]
Materials:
Paper: [PDF 15.6M].
Supp: [ZIP 49.8M].
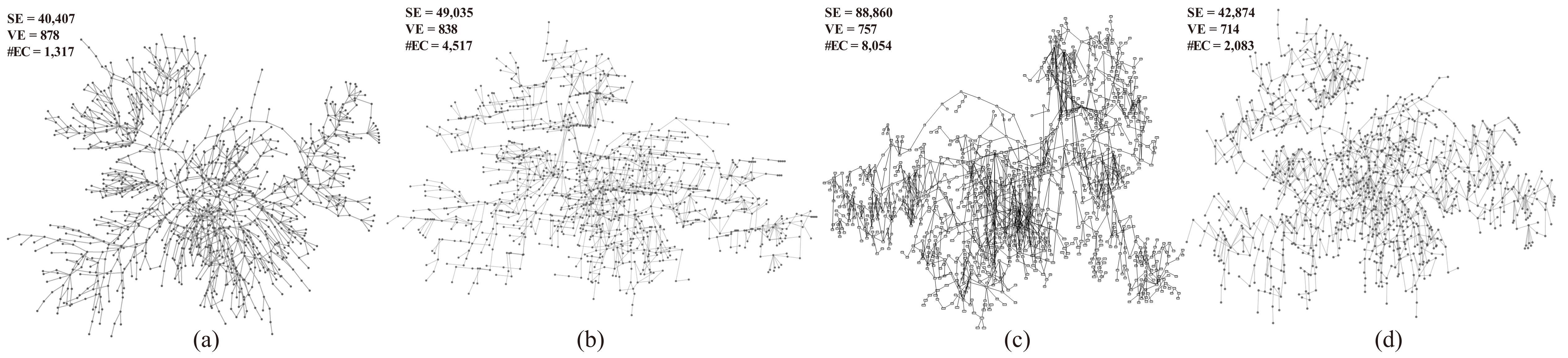
Figure 2: Comparison of the layout of the Bus1138 graph data with downward constraints generated by different methods: (a) unconstrained stress majorization (UC); (b) IPSep; (c) SV; and (d) our method with weight vij set to be 4.
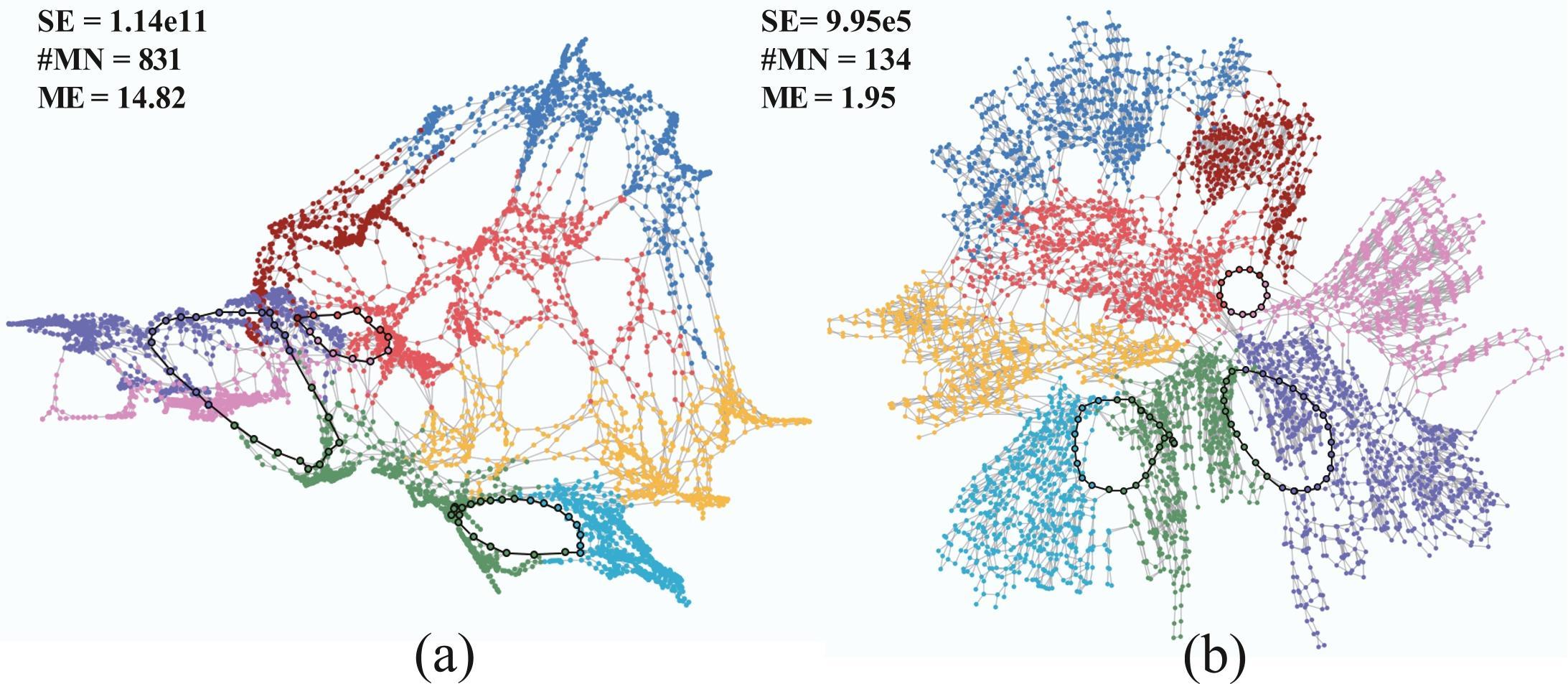
Figure 3: Comparison of the layout of Bcspwr10 with cluster non-overlap and circle constraints generated by SV (a) and our method with vij set to 3.5 (b).
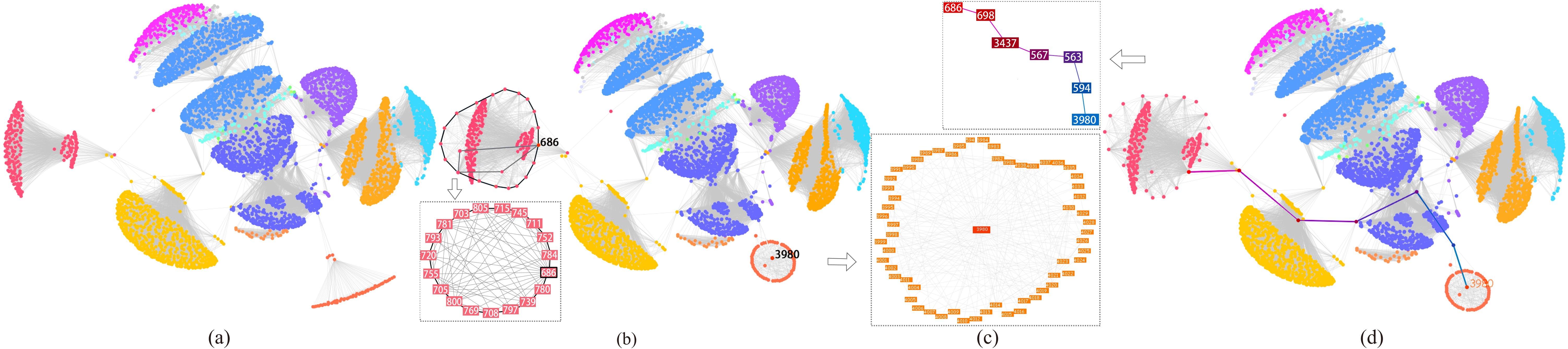
Figure 4: Exploration of circles in the Ego-network. (a) results generated by using cluster non-overlap constraints, where 16 communities are separated; (b) results generated by enforcing circle and star shapes to two selected nodes: 686 and 3980, the highlighted sub-graphs are shown in the detail views. (c) results generated by enforcing path constraints to these two nodes, the detailed node label information is shown in the detail view.
Acknowledgements:
The authors would like to thank Zeyu Wang and Tong Ge for their help in making the video, and the anonymous reviewers for the valuable comments. This work is supported by the grants of NSFCGuangdong Joint Fund (U1501255), the National Key Research & Development Plan of China (2016YFB1001404), National Foreign 1000 Talent Plan (WQ201344000169), Leading Talents of Guangdong Program (00201509), Shandong Provincial Natural Science Foundation (2016ZRE27617), Shenzhen Science and Technology Program (JCYJ20170413162617606), and the Fundamental Research Funds of Shandong University.